Contents of example

Example

Integrate-system integrates the system

y_k^′ = f_k(y₁, y₂,…, y_n), k = 1,…, n

of differential equations with the method of Runge-Kutta.

The parameter system-derivative is a function that takes a system state (a vector of values for the state variables y₁,…, y_n) and produces a system derivative (the values y₁^′,…, y_n^′). The parameter initial-state provides an initial system state, and h is an initial guess for the length of the integration step.

The value returned by integrate-system is an infinite stream of system states.

$\begin{schemenoindent} (define integrate-system (lambda (system-derivative init... ...l-state (delay (map-streams next states))))) states))))% \end{schemenoindent}$

Runge-Kutta-4 takes a function, f, that produces a system derivative from a system state. Runge-Kutta-4 produces a function that takes a system state and produces a new system state.

$\begin{schemenoindent} (define runge-kutta-4 (lambda (f h) (let ((*h (scale-ve... ...-vector (lambda (s) (elementwise (lambda (x) (* x s)))))% \end{schemenoindent}$

Map-streams is analogous to map: it applies its first argument (a procedure) to all the elements of its second argument (a stream).

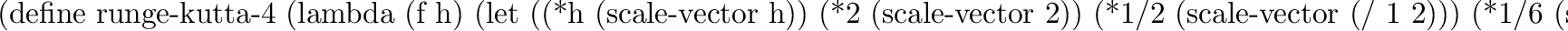
$\begin{schemenoindent} (define map-streams (lambda (f s) (cons (f (head s)) (delay (map-streams f (tail s))))))% \end{schemenoindent}$

Infinite streams are implemented as pairs whose car holds the first element of the stream and whose cdr holds a promise to deliver the rest of the stream.

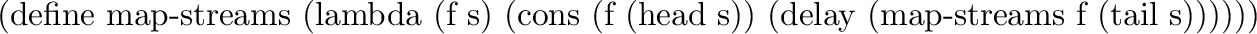
$\begin{schemenoindent} (define head car) (define tail (lambda (stream) (force (cdr stream))))% \end{schemenoindent}$

The following illustrates the use of integrate-system in integrating the system

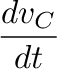
C $\displaystyle {dv_C \over dt}$ = - i_L - $\displaystyle {v_C \over R}$

L $\displaystyle {di_L \over dt}$ = v_C

which models a damped oscillator.

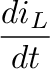
$\begin{schemenoindent} (define damped-oscillator (lambda (R L C) (lambda (stat... ...(damped-oscillator 10000 1000 .001) '\char93 (1 0) .01))% \end{schemenoindent}$

Show some output?